Drunkard’s walk

We can generalize the idea a little bit into the two-dimensional case. Suppose we have a drunk guy leaving a bar. The guy is drunk to the suitable level that he can keep the size of each step but lose the ability to be oriented. So the direction of each step is random. We can use a randomly oriented vector of length \(L\), \(\textbf{l}_j=L(\cos\theta_j,\sin\theta_j)\), to denote the \(j\)-th step of the drunk guy. By definition, we also have \(\langle \textbf{l}_m\cdot\textbf{l}_n\rangle=L^2\langle\cos(\theta_m-\theta_n)\rangle=0\) since \(\theta_m\) and \(\theta_n\) are random angles.

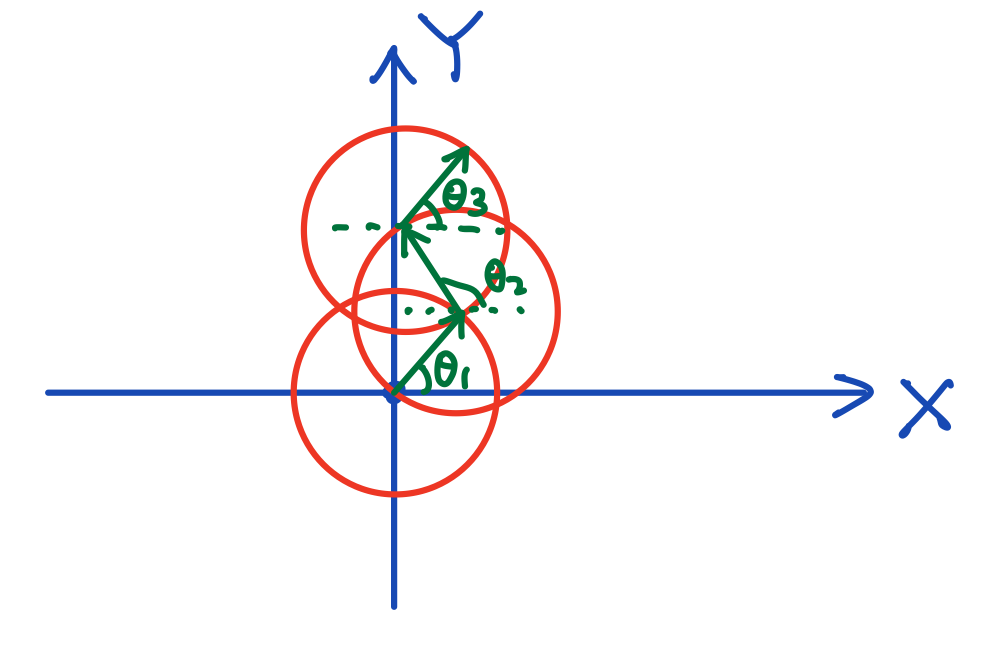
_images/2D_RW_4.png — Fig. 6 Two-dimensional drunkard’s walk.

What?

What is the probability for a specific value of \(\theta_j\)? That is, what is \(P(\theta_j)\)?

Similarly, we can define the position of the drunk guy after \(N\) steps as

\[ \textbf{X}_N=\sum_{j=1}^{N}\textbf{l}_j. \]

We can evaluate \(\langle \textbf{X}_N\rangle\) as following

\[ \langle \textbf{X}_N^2\rangle\equiv\langle (\textbf{X}_{N-1}+\textbf{l}_N)^2\rangle=\langle (\textbf{X}_{N-1})^2\rangle+\underbrace{\langle (\textbf{l}_{N})^2\rangle}_{L^2}+2\underbrace{\langle \textbf{X}_{N-1}\cdot\textbf{l}_N\rangle}_{=0}=\langle \textbf{X}_{N-1}^2\rangle+L^2. \]

Iterate this relation, we have

\[ \langle \textbf{X}_N^2\rangle=NL^2 \]

and

\[ \sigma_{\textbf{X}_N}=\sqrt{N}L. \]

To compare with our previous one-dimensional case, we can set \(L=1\), and we have \(\sigma_{\textbf{X}_N}=\sqrt{N}\). From here, we can also generalize the idea into \(D\) dimensional randomly oriented walk with a unit step size. The r.m.s should also be \(\sqrt{N}\).

If we ask the question in a reverse way: what kind of path will be (statistically) away from the origin with distance \(\sqrt{N}\) after \(N\) steps? The answer will be the randomly oriented path.

Another interesting point to notice is we start from the one-dimensional case. Then, we modify our problem by considering additional dimensions. If we keep the assumption that the orientation of the higher dimensional case is also random, we will always have the r.m.s behavior of \(\sqrt{N}\).